Hi everyone! For the first math seminar of the semester, I will be discussing the idea of a Cantor Polynomial and an interesting theorem that relates to these polynomials called the Fueter-Polya Theorem. Cantor Polynomials deal with the question of taking multi-dimensional data and storing it in a linear manner. Think about how we might store a large matrix into the linear memory of a computer. This is essentially what the Cantor Polynomials help us do. In my talk, I will discuss this problem in a little more detail, uncover what exactly the Cantor Polynomials are, and mention several different related results, conjectures, and areas of further research that mathematicians are currently working on.
In terms of the mathematical concepts needed to understand this talk, the idea of injective, subjective, and bijective functions play an important role. Here is a link to a site with an explanation of these concepts in case you are unsure. Otherwise, the idea of a group from abstract algebra is also included, but we will spend time defining a group if you haven’t taken that course yet. To help you think about our question before my talk, I leave you with an image. Think about Cantor’s diagonalization argument from MAT 230. A similar argument may help us here. I look forward to presenting this topic to everyone on Wednesday!
Here is a figure at this link.
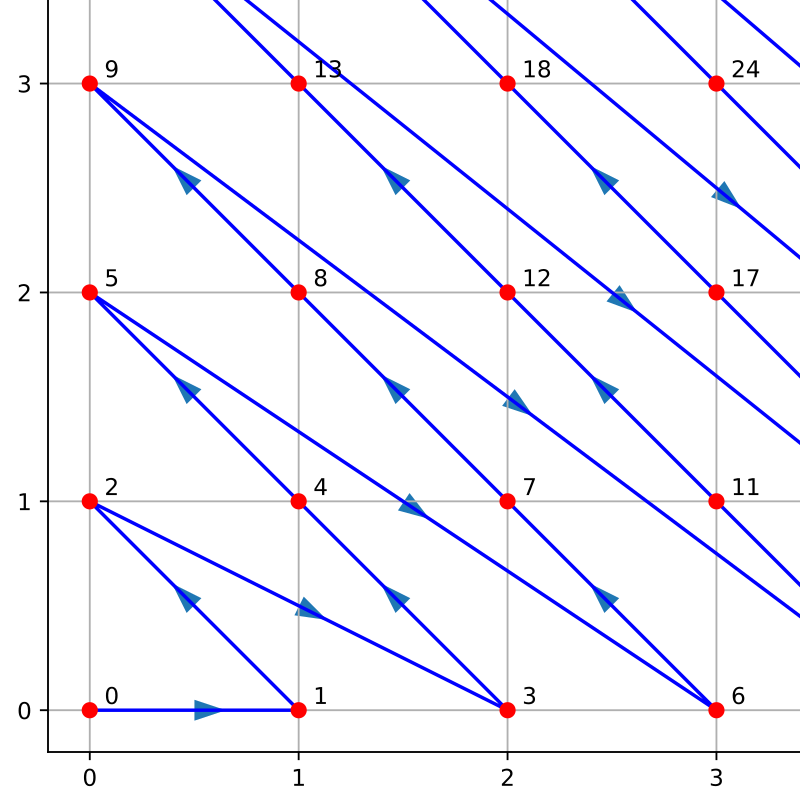

Thanks for your nice post, and thanks for suggesting that I help with the image; we will try to make posting simpler as we go along.
I thought this was a really good presentation and now I really want to see if our discussion about a bijection on all integers is also possible.
I found this presentation helpful and as well informative. I never thought that people would store data from left to right and up to down on the computer especially when it was related to Cantor Polynomials. It was a very interesting presentation, keep up the good work.
Cantor Polynomials are rather interesting.