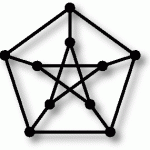
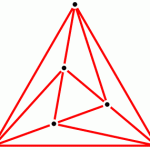
Kuratowski’s Theorem may be stated as follows:
Let 
be a graph. is nonplanar if and only if contains a subdivision of either 
or 
as a subgraph.
In the talk, we use the following definition of a graph:
Let 
and 
be sets. 
is a graph if and only if it satisfies the following conditions:
1) 
(edges),
2) for all 
, 
(no loops), and
3) 
implies 
(edge symmetric).
Elements are called vertices and 
are edges. As is edge symmetric (that is, it satisfies our third criterion above), it will be expedient to refer to both 
as the same object 
.
A graph is said to be planar if and only if there exists an isomorphic planar embedding of the graph in 
. That is, is planar provided it can be drawn in the euclidean plane such that edges of the graph cross precisely when there is a vertex, and nowhere else.
It will be necessary to include further definitions in the talk. However, for the moment, these capture the structures with which we shall be dealing.
We begin by motivating the idea of a nonplanar graph with an interesting puzzle. From here, I shall provide a simple proof of the sufficiency of Kuratowski’s Theorem and a sketch of a proof of the necessity, as well as complete proofs of several other related results.
Sources: Bondy, J. Graph Theory. New York: Springer, 2008.